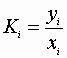
Bubble Point
Dew point
We may define the physical equilibrium constant, Ki:
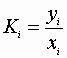
At lower pressures (<10 bar) the fugarity coefficients in each phase are nearly equal:
![]()
And at these pressures the Poynting factor » 1:
![]()
![]()
I
![]() II
II
![]() And:
And:
III
To find the dew point pressure at a given T and Y:
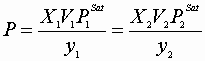
IV
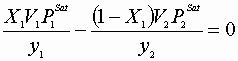 Or:
Or:
V
Solve IV for X1, and then V for P, since Vi=f(xi) This may have to be done iteratively.
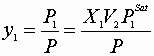
B-3 Missing
V. Flash calculations:
All Zi,P, and T are known; find X’s, y’s, and V,L
![]()
Here:
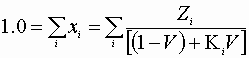
And:
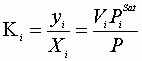
Therefore, for each component:
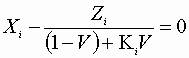
![]() Plus:
Plus:
We must iteratively find the roots which satisfy all of the n + l equations.
Example Calculations:
P1Sat = 323.5 mmHg P2Sat = 537.1 mmHg
We also know the Von Laar coefficients:
A = 2.41 B = 1.97
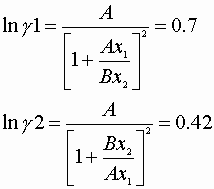
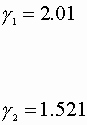
![]()
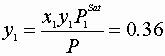
Wilson
Antoine’s
Wilson correlation:
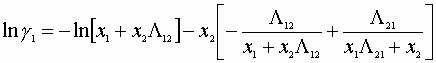
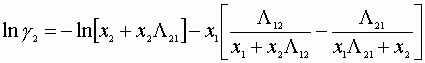
We must satisfy 3 equations:
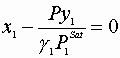
Initial guesses x1=x2=0.5
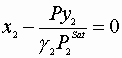
![]()
Solution:
x1=0.811 P=0.3443barGiven: Wilson Parameter:
![]()
![]()
Without TBP we do not know PSat’s!
Solution must satisfy:
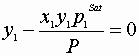
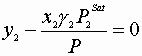
![]()
Guess y’s & TBP:
Try y=0.5 T=373
Solution:
y1=0.353 T=361.6K![]() experimental
experimental
Wilson Parameters: ![]()
![]()
Criteria that must be satisfied:
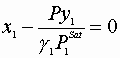
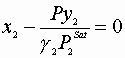
![]()
Now with x1, x2, and T unknown. (Roots found are sensitive to initial guesses)
If we guess x=0.5 T=350K
Solution: x1=0.555 T=332.1K
A 40 mol% isobutane 160 mol%n n-pentane mixture flows into a flash chamber ad flashes at 49° C and 3.2 bar. Find how much gas and liquid leave per mole of feed, and find the composition of both streams.
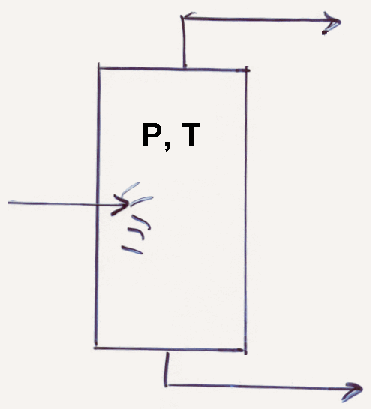 Here:
Here:
Determine K i’s
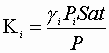
![]()
![]()
Also
![]()
![]()
Choose a basis of 1 mole feed/s. Here we must solve the following criteria:
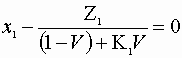
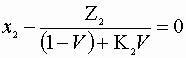
![]()
![]()
Guess a value for V, solve for x1 and x2 from
1 & 2: Determine if this satisfies 3. (A table may help)Solution:
L = 0.8 x1 = 0.33 x2 = 0.67
V = 0.2 y1 = 0.67 y2 = 0.33
All of these methods become easy with root finding methods. (See MathCad handout)
Adiabatic Flash

Here the energy balance must be used in conjunction with the mass balance and equilibrium criteria!
(remember Hvgs!)![]()
![]()
![]()
![]()
Since we do not know T, x’s, or V we must solve the equation
A in conjunction with the previous flash criteria.![]()
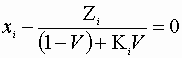
Here: 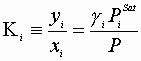
For a binary system this gives us 4 equations and 4 unknowns. Also the modified Raoult’s Law requires an expression for PiSat(T)and g i(T).
We will also require Cp’s DHvgs’s,
(rigorously as f(T), but seldom all available.) Then we may solve the 4 equations iterativey until the proper roots are found.Phase Equilibrium from EOS
Extrapolation of the activity coefficient approach to highter T & P’s may not be possible since:
![]()
![]()
We may no longer ignore ![]() and The
and The
Poynting factor. Instead we might directly use fugacity coefficients for both phases, ![]() and
and ![]() .
.
At equilibrium:
![]()
Here, we have 5 unknowns: (for binary)
Y’s, V’s, P; when we calculate a Pxy diagram:
To find the molar volumes:
(using Redlich-Kuvorg)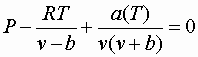
There will be 3 roots: liquid v, vapor v, and an "unreal" middle root.
We typically use mixture rules to get am and bm for the EOS to find these roots. This allows us to solve the fugacity forms of the EOS for ![]() and
and ![]() . Finally, for a binary mixture we must satisfy the criteria:
. Finally, for a binary mixture we must satisfy the criteria:
1 ![]()
2 ![]()
Starting at ![]() ,
, ![]() , we may determine the entire composition pressure diagram. We may similarly substitute
, we may determine the entire composition pressure diagram. We may similarly substitute 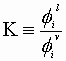 for flash calculations.
for flash calculations.
Multicomponent Mixture
Both the Wilson an NRTL equations are readily extended to manyu components.
Example: Find the dew point pressure and liquid phase mole fractions for a vapor mixture of acetone (1), methylacetate (2), and methanol (3) at 323K.
Given: ![]()
![]()
![]()
We also need 6 Wilson parameters to determine a ternary mixtures properties.
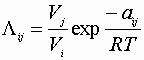
From aij’s for each binary composition:
![]()
![]()
![]()
![]()
![]()
![]()
Start B-16