Lecture 1:
Introduction to Thermodynamics Role of thermodynamic Principles in real-life situations active learning and attitude of a true student Course Outline Syllabus
- System, Definition and Types of Systems Closed, Open, Isolated; System properties
Lecture 2:
- Postulates of Thermodynamics:
- (n+2) rule
- Existence of stable equilibrium
- State
- Point and Path Functions
- Work
- Deriving expression for Work from first principles (force balance)
- Adiabatic work interactions (most direct path from one point to another)
- Postulate III of Thermodynamics: Change of state is possible in at least one route and the adiabatic work is identified from the corresponding end states
Lecture 3:
- Definition of Heat
- Postulate IV of Thermodynamics or Zeroth Law of Thermodynamics: A&B are in equilibrium; B&C are in equilibrium, then A&C are in equilibrium
- First law of Thermodynamics: dQ = dU + dW; importance of sign conventions
- First law as applied to closed systems
- Ideal gas concept applied to gases; Enthalpy, Internal Energy and relation between the heat capacities of gases
Lecture 4:
- First law as applied to open systems
- Work refinements Types of Work: Electrical, Mechanical, Surface Tension, Elastic, Kinetic Energy, Rotational Relativistic
- Additional Enthalpies
- Sensible Heat
- Latent Heat: -Change of Phase, Chemical Reaction, Nuclear Reaction
Lecture 5:
Flow Systems:
Force balance on steady-state, steady flow systems
- Isothermal Expansion
- Converging Nozzle
- Heat Exchanger
- Adiabatic periodic piston
- Ideal isothermal turbine
- Ideal adiabatic turbine
Lecture 7:
Work Energy cycles with examples Flow Systems Batch
systems Bernoulli equation as a special case of 1st law of
thermodynamics
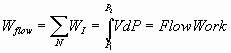 ;
;
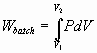
Ideal Isothermal Turbine
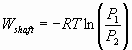
The difference in the work produced in an adiabatic batch
vs. flow system is related to the difference in D H
& D U = D (PV)
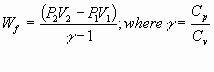
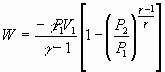
= -nCp (T2-T1)
Example 4: Adiabatic Expansion @ Constant Volume
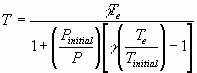
For P >> Pintial; T
ΰ g Te
Lecture 8:
Definition of Path Function
Part II of Example 4 Constant Adiabatic Expansion @
Constant Pressure
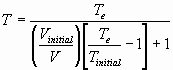
Example 8 Home Work problem 2.32: Real Gas work:
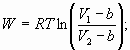 Isothermal batch
systems Home Work Problem 2.29:
Isothermal batch
systems Home Work Problem 2.29:
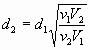 ; H2-H1
=
; H2-H1
=  (v12-v22)/2
(v12-v22)/2
Lecture 9:
Historical approach to the second law of thermodynamics
Carnot (heat engine) and Clausius (entropy)
Examples demonstrating the Entropy phenomena, Concept of
Equilibrium, Heat and Work
Definition of Reversible process Rankine cycle
Concept of Thermodynamic Temperature
Lecture 10:
Definition of Thermodynamic Efficiency (h
) and its derivation
Introduction to Entropy Definition, Concept of Entropy
from heat engines
For any isolated system D Ssystem
³ 0;
For any system D Ssystem+D
Ssurroundings ³ 0
Homework Problems: 5.5, 5.8, 5.14
Entropy and 2nd law of Thermodynamics
Definition and derivation of thermodynamic efficiency Efficiency limits
functionality
Carnot Cycle: Definition and derivation of Carnot
efficiency
Clausius Theorem: Any process can be broken into
equivalent adiabatic and isothermal steps
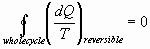
For a process with less than a complete cycle, entropy is defined as:
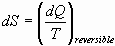
Entropy is a state function; Entropy of the Universe is never conserved
Lecture 11:
Combined 1st and 2nd law of Thermodynamics:
Conservation of Energy with respect to Entropy
Ideal gases and 2nd law of Thermodynamics: Isochoric process,
Isobaric Processes, Isothermal processes, Processes from (P1, V1,
T1) to (P2, V2, T2) with respect
to Entropy and Adiabatic reversible processes: Isentropic processes
(n+2) rule for a single phase system with respect to Entropy
Examples of Second law of Thermodynamics, Reversible work, to calculate
change in Entropy: Bird problem, Hilsch tube etc.
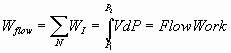 ;
;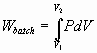
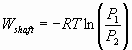
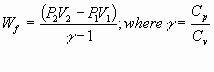
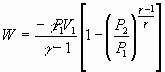

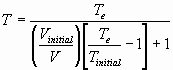
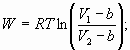 Isothermal batch
systems Home Work Problem 2.29:
Isothermal batch
systems Home Work Problem 2.29:
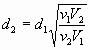 ; H2-H1
=
; H2-H1
=