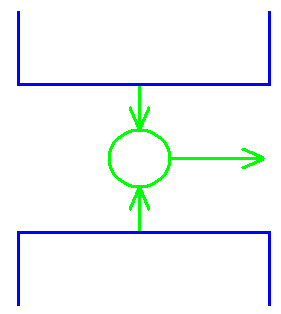
Entropy – 2nd Law

Definition of thermodynamic efficiency:

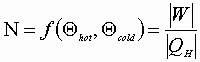
or

 

 

 

 

 

 

 

 

 

 

 

 

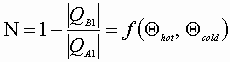
Consider a Carnot cycle: (page 157 5th Ed.)

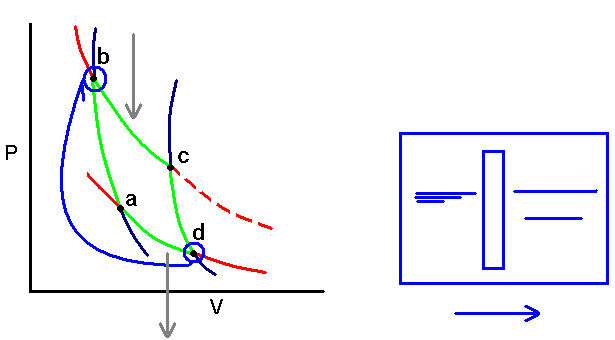
For the isothermal steps:

A)

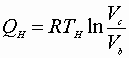
B)

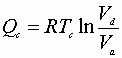
From the adiabatic steps:

Since and

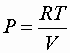
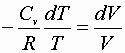
Integrating a® b or c® d:

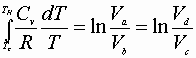
Then:

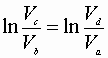
From A) & B):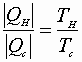

Substitution for Neqn:

 

 

 

 

 

 

 

 

 

 

 

Arbitrary work path:

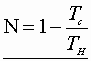
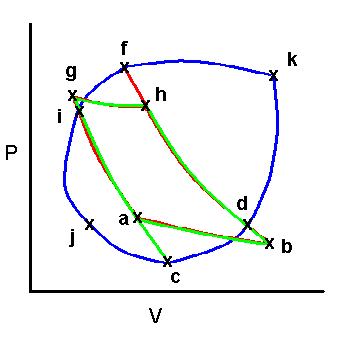
Clauusius’ theorem – any process can be broken into equivalent isothermal & adiabatic steps!

Therefore as before we can sum over the cycle:

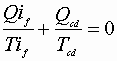
or for many tiny cycles to sum up:

 

 

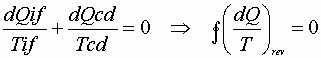
Over less than a whole cycle the integral may not be zero;

Then:

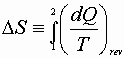
or

  1. Entropy is a state function, & therefore, although we calculate D S from a hypothetical reversible process, it is identical in an equivalent irreversible process.
  2. Entropy of the universe is not conserved:

 

 

 

Combined 1st & 2nd Law

  1. Energy conserved – 1st Law

    (neglect PE & KE)

  2. Entropy is defined as: 2nd Law

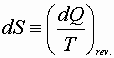
  3. Combined 1st & 2nd Law:

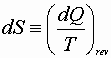
Substitute for dQ

or

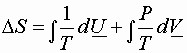
or

 

 

Ideal Gasses & 2nd Law

1) Constant volume process:

  1. Constant Pressure processes:

.

  1. Constant temperature process:

  2. Going from P1V1T1 to P2B2T2:

 

 

Or in terms of T, V: (T1V1® T2V2)

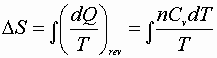
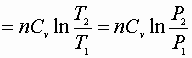
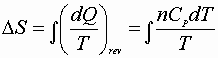
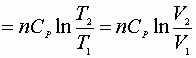
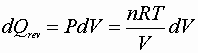
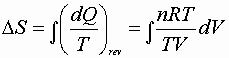
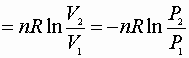
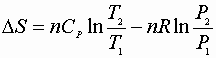
P, V: (P1V1® P2V2)

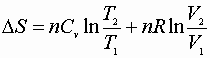
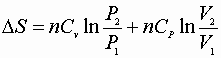
Since D S is a state function these can be used for any path!

Adiabatic reversible processes

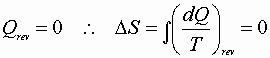
Isentropic process!