Return
to Homework page | Return
to CM3110 Homepage
Homework 4
CM3110 Transport Processes I
CM3110
-
Show for Newtonian fluids in laminar flow that the Fanning friction
factor,
f,
is given by f=16/Re, where Re is the Reynolds number.
SOLUTION
-
(Calculate flow rate from pressure
drop
- tube flow) For a pipe (inner diameter = 2.00 in) water at 25oC
(density = 62.4 lbm/ft3, viscosity = 6.7197 X
10-4 lbm/(ft s)) is made to flow under a pressure drop per
unit
length of 1.90 X
10-2psi/in. What will be the average velocity of the
water
in the pipe? Is the flow laminar or turbulent? What would the
pressure
drop need to be for the flow to change from laminar to fully turbulent
(or from turbulent to laminar, whichever is appropriate)? SOLUTION
METHOD ONE. Also I solved it a second, similar way: ALTERNATE
SOLUTION METHOD
-
(Macroscopic momentum balance -
Tube
flow) Using our nomenclature for doing macroscopic momentum
balances,
calculate the force on the walls for steady, turbulent flow of an
incompressible
newtonian fluid through a straight pipe. Assume that the flow is
downward, i.e. in the direction of gravity. Note that the answer
obtained is the same as performing a force balance, which we did when
calclating
the relationship between pressure and friction factor (see
lecture 10). SOLUTION
-
(Flow through an expanding bend) Geankoplis, 3rd edition,
2.8-4,
page 110 . Water at a steady state flow rate of 0.050 m3/s
is flowing through an expanding bend that changes direction by 60o.
The upstream diameter is 0.0762 m and the downstream diameter is
0.2112m.
The upstream pressure is 68.94 kPa (gage pressure). Calculate the
downstream pressure and the vector force on the bend. The entire
apparatus is at 298K and you may neglect energy losses in the bend. SOLUTION
-
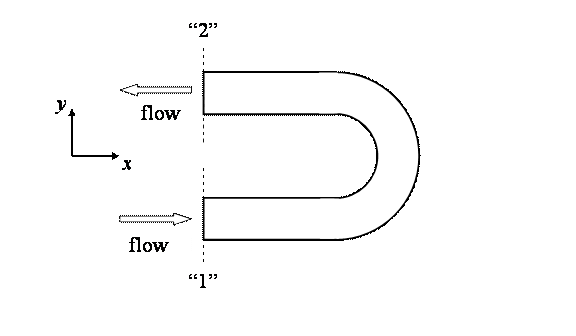
(Force on a U-Tube) Bird,
Stewart,
and Lightfoot, Transport Phenomena (Wiley, 1960) plm 7.D1. Water
is flowing in a horizontal, U-shaped tube. The flow is turbulent,
the inner diameter of the tube is 4.00 in, and the fluid is water at
68.0oF
(density = 62.4 lbm/ft3, viscosity = 1.00 cP, flow rate =
3.00
ft3/s). The pressure at surface "1" is 21 psia, and
the
pressure at surface "2" is 19 psia. What is the total force on
the
bend? SOLUTION
-
(Flow in noncircular conduits)The
frictional losses in non-circular conduits are found to follow the same
data correlations (friction factor versus Reynolds number) as flow
through
circular conduits if the equivalent hydrodynamic diameter DH
is used instead of the regular pipe diameter D both in the definitions
of Re and of Fanning friction factor (See Geankoplis 3rd edition p99 or
Denn or Perry's Handbook). DH , which is equal to four
times the hydraulic radius RH (weird, but true), is equal to
four times the ratio of (cross-sectional area of the conduit) to
(wetted
perimeter of the conduit). Calculate the equivalent hydraulic
diameter
for an annular conduit with inside diameter D1 and outside
diameter
D2. Calculate the equivalent hydraulic diameter for a
rectangular duct of sides a and b. What is the pressure-drop per
unit length for room-temperature water flowing at 3 ft3/s in
an annular conduit? The inner diameter is 2.0 inches, and the
outer
diameter is 5.0 inches. SOLUTION
-
(Practical Issues) Please
answer
the following questions: SOLUTION
-
What is the difference between schedule 40 and schedule 80 pipe?
-
At what value of Reynolds number does the transition from laminar to
turbulent
flow occur in pipes?
-
What is the roughness of commercial steel?
-
The chart on page 88 of Geankoplis 3rd edition gives values of Fanning
friction factor
versus Reynolds number for flow in a tube. We showed in class that
dimensional
analysis of the equations of change tells us that friction factor is
only
a function of Reynolds number (for flows without free surfaces). Is the
analysis we carried out to arrive at that conclusion valid for the flow
of gasses in pipes? Why or why not?
Return
to Homework page | Return
to CM3110 Homepage

