Example:

with initial condition, x(0)=5 and all higher derivatives of x are zero at t=0
Step 1. Obtain the characteristic equation:

4s5 + 20 s4 + 53 s3 + 96 s2 + 93 s + 34 = 0

Step 2. Solve for the roots: { -2, -1, -1, -0.5+2i, -0.5-2i }

Step 3. Form the complementary solution,

xc (t) = A1 e-2t + A2 e-t + A3 t e-t + A4 e-0.5tcos(2t) + A5 e-0.5t sin(2t)

Step 4. Form the particular solution,

xp (t) = D1 t2 e-t + D2 cos(2t) + D3 sin(2t)

Step 5. Take the derivatives of xp(t),

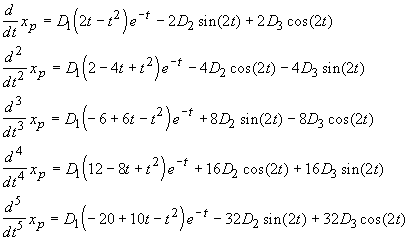
Step 6. Substitute these derivatives into original equation, then equate coefficient on both sides,

34 D1 = -3
-30 D2 - 110 D3 = 5
110 D2 - 30 D3 = 0

and obtain the unknown coefficients: D1 = -0.0882, D2=-0.0138 and D3=-0.0459
Step 7. Evaluate arbitrary coefficients.

                x = xc + xp

                    = A1 e-2t + A2 e-t + A3 t e-t + A4 e-0.5t cos(2t) + A5 e-0.5t sin(2t)
                       - 0.0882 t2 e-t - 0.0115 cos(2t) - 0.0423 sin(2t)

and applying the initial conditions,


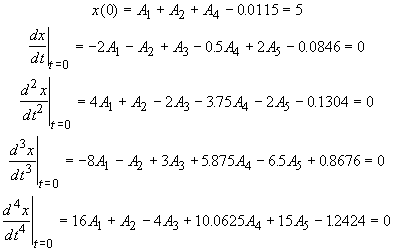
Next, solve these 5 equations simultaneously to get A1=3.4639, A2=2.3387, A3=10.0673, A4=-0.7888, A5=-0.5517. So finally, the complete solution is given by
            x = 3.464 e-2t + 2.339 e-t + 10.067 t e-t – 0.788 e-0.5t cos(2t) – 0.5517 e-0.5t sin(2t)
                - 0.0882 t2 e-t - 0.0115 cos(2t) - 0.0423 sin(2t)

Step 8. Plot the result to observe the trajectory.




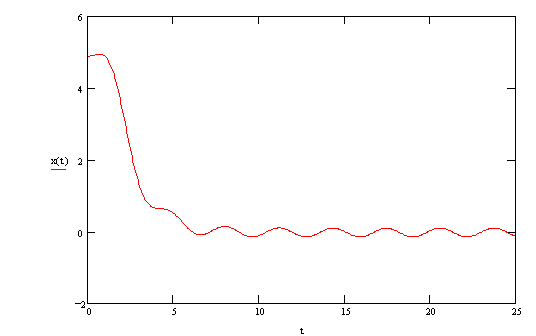
Click here to go back to the short review on solving ODEs

This page is maintained by Tomas B. Co (tbco@mtu.edu). Last revised 11/29/1998.

     Tomas B. Co
     Associate Professor
     Department of Chemical Engineering
     Michigan Technological University
     1400 Townsend Avenue
     Houghton, MI 49931-1295

Back to Homepage