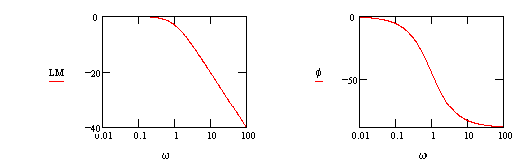
1. First order lag:
1. First order lag: ![]()
2. First order lead: G(s) = t s + 1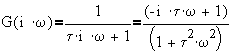
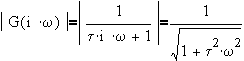
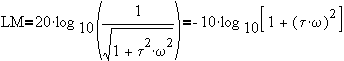
@ low frequency, LM=0
@ high frequency,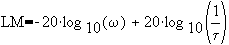
which is a line whose slope is -20 db/decade and an "x-intercept" at w=1/t. @ w=1/t, LM=-10 log10( 2 )= -3.01 dB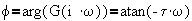
@ low frequency, f=0 @ high frequency, f= -90o @ w=1/t, f= -45o slope= -66o/decade
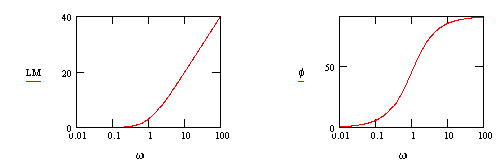
@ high frequency, LM=20 log10( w ) + 20 log10( t )
@ high frequency, f=90o
@ w=1/t, f=45o
slope= 66o/decade
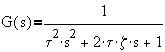 (z<1)
(z<1)
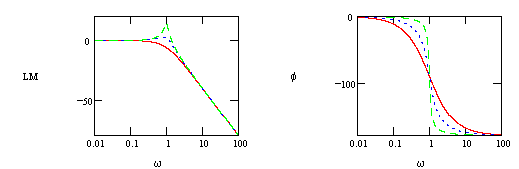
@ low frequency, LM=0
@ high frequency,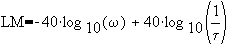 which is a line whose slope is +40 db/decade and an "x-intercept" at w=1/t.
which is a line whose slope is +40 db/decade and an "x-intercept" at w=1/t.
To determine the peak, take derivative of LM with respect to w and then set to zero.
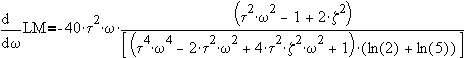
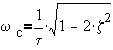 ®
® 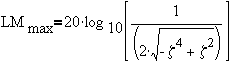
@ low frequency, f=0o
@ high frequency, f=180o
@ w=1/t, f=180o
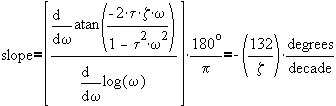
4. Delay: ![]()
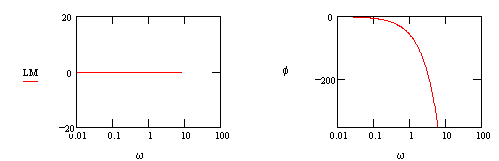
LM=0
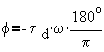 @ w=1/td f = -57.3o
@ w=1/td f = -57.3o
@ w=2/td f = -114.6o
@ w=3/td f = -171.9o
5. Integrator: ![]()
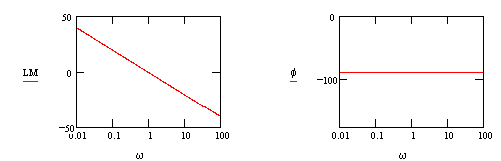
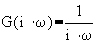
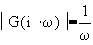
: line with a slope = - 20dB/decade
@ w=1 LM=0
5. Differentiator:
G(s) = s
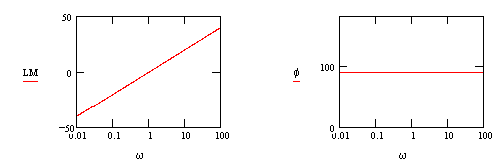
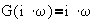
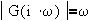
: line with a slope = + 20dB/decade
@ w=1 LM=0
Frequency Plots of Higher Order Transfer Functions
Let G(s)= G1(s) G2(s)
![]()
In polar form,
= ![]()
thus,
In terms of log modulus,1) arg(G) = arg(G1) + arg(G2) or f = f1 + f2
2) | G | = | G1 | | G2 |
= ![]()
or LM( G ) = LM( G1 ) + LM( G2 )
Implications:
1) Putting a constant gain K in series with G means | KG | = | K | | G | and
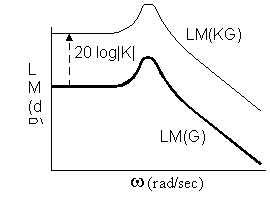
Log modulus plot is translated vertically upward if | K | > 1 (downward if | K | < 1)
Since arg(K)=0, the phase shift vs frequency plot remains unchanged.
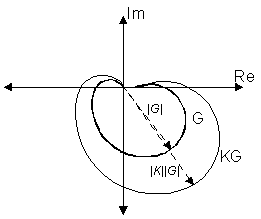
The Nyquist plot expands proportionally away from origin if |K| > 1 ( and shrinks if |K| < 1)
2. At high frequencies, every polynomial order in the denominator contributes -90o in the phase shift plot; while every polynomial order in the numerator contributes +90o.3. Using rough line segments for approximate plots, various lead and lags can be combined to produce desired "reshaping" of transfer functions.
Example:
The "real" PID has the transfer function
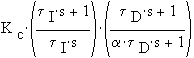
Adding the following log modulus plots:
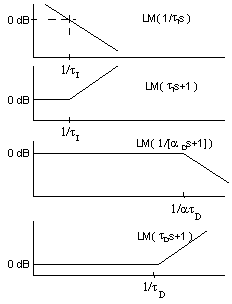
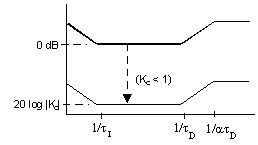
yields
This page is maintained by Tomas B. Co (tbco@mtu.edu).
Last revised 2/10/1999.
Tomas B. Co
Associate Professor
Department of Chemical Engineering
Michigan Technological University
1400 Townsend Avenue
Houghton, MI 49931-1295