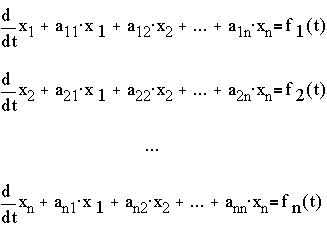
Linear First Order ODEs
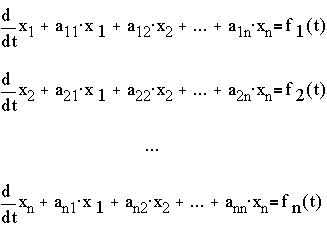
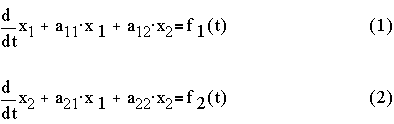
Step 1: take derivative of (1),
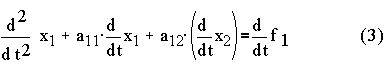
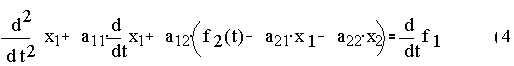
Step 3: From (1), get x2 in terms of x1
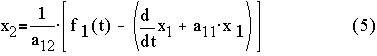
Step 4: Substitute (5) into (4) and rearrange
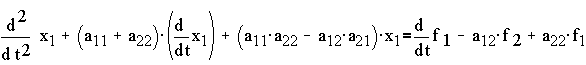
Thus the characteristic equation will be given by
![]()
Note: If we had tried to find a second order differential equation in terms of x2 using the same procedure of substitution, we will obtain
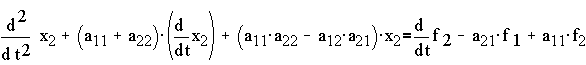
which will yield the same characteristic equation. Thus
there is really just one characteristic equation for the system.
The eigenvalues will just be the roots of the characteristic
equation.
Example:
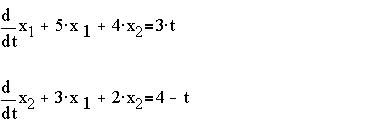
Then the characteristic equation and the eigenvalues are:
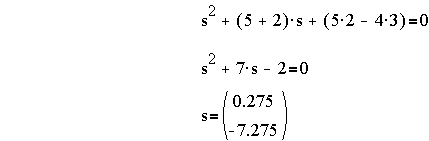
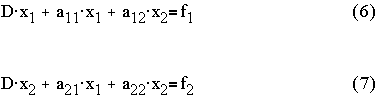
Step 2: Extract the matrix operator,
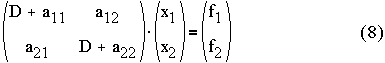
Step 2: Use Cramer’s rule,
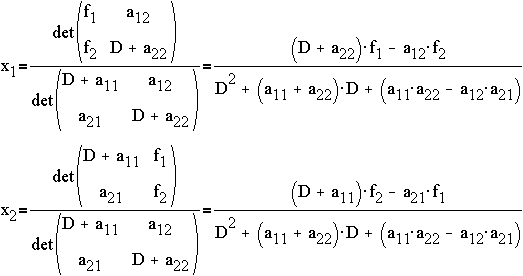
or,
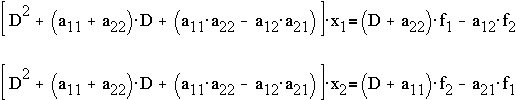
which is the same result as Method 1 when D is replaced
back by d/dt.
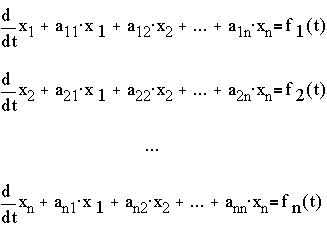
can be obtained as
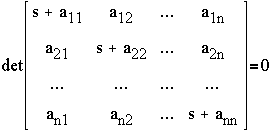
Example:
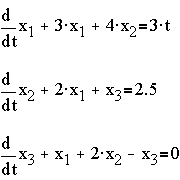
The characteristic equation and the eigenvalues are given
by
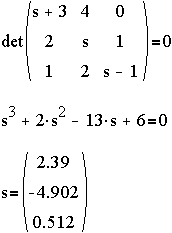
The system is unstable.
This page is maintained by Tomas B. Co (tbco@mtu.edu). Last revised 12/10/1999.
Tomas B. Co
Associate Professor
Department of Chemical Engineering
Michigan Technological University
1400 Townsend Avenue
Houghton, MI 49931-1295