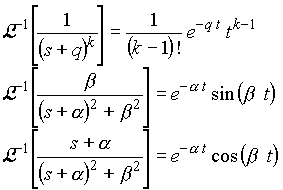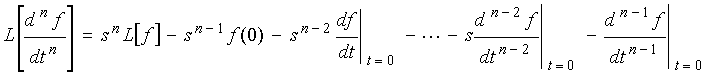
I. Important Properties of Laplace Transforms:

1. Linearity:        L[af(t)+bg(t)] = aL[f(t)] + bL[g(t)]

2. Nth Order Derivative:

3. Integral

4. First Shifting Theorem:

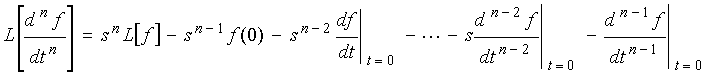
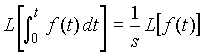
5. Second Shifting Theorem: Let f(t)=0 for t<0,

II. Solution of Linear Differential Equations:

Given : A linear differential equation of x(t) with all the necessary initial conditions.
Procedure:

1. Take Laplace transform of both sides of the differential equation
2. Substitute given initial conditions where needed.
3. Rearrange the equation so that X(s) is equal to a rational polynomial function in s, i.e. a function whose numerator and denominator are polynomials in s.
   (Note: the order of the numerator polynomial should be smaller than the order of the denominator polynomial.)
1. Use the method of partial fractions to separate X(s) into various terms in which the table of Laplace transforms can be used to obtain the inverse transform.
2. Perform the inverse transforms. (Simplify if desired).

III. Method of Partial Fractions to find inverse Laplace transform
 
Given:  f(s) = num(s)/den(s)
 
where num(s)=numerator polynomial in s, den(s)=denominator polynomial in s


Step 1: Find the roots of the denominator polynomial, say  - r₁,  ... ,  -r_N

Step 2: Based on these roots separate num(s)/den(s) into partial fractions.
 

Case 1: For each root, say -q, appearing k times, add the following k terms:




Case 2: For each complex pair of roots, say -a+ib and -a-ib, add two terms:


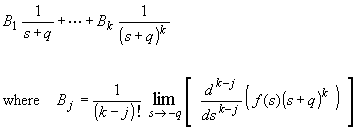
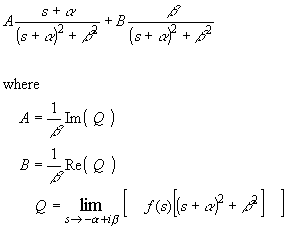
Step 3. If needed, take the inverse Laplace transforms of each terms using the following formulas: