The Fundamental Equation:

Where:

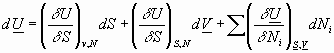
and:

or:

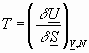
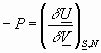
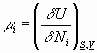
These are the starting point for EOS:

Now take the derivative of the above with respect to other independent variables:

 

 

 

 

 

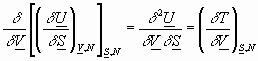
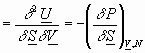
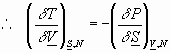
If we differentiate w.r.t: S,etc. we get:

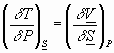
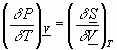
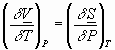
There are similar arguments for D H, D G, D A, electromagnetism, gravity, etc.:

Eg: --- Given:

and:

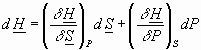
etc!

What other relationships do we have to work from?

 

If we recognize that each property such as P, T, V, etc. can be used in our n + 2 postulate. It can be shown via "Legendre Trasformations" that a derivative can replace these values in our description:

These lead to the rest of the thermodynamic identities and a few definitions:

There are 3 Legendre transforms of the fundamental equation:

2 first order transforms: (one variable changed)

1 second order transform:

 

 

 

 

 

 

Or in differential form:

Now we have the ability to define the remainder of our identities:

Eg:

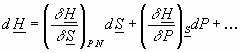
From previous page: =T =V

To summarize:

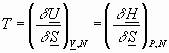
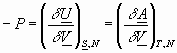
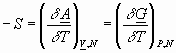
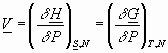
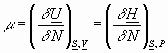
etc.

One final transform:

or

Additional useful relationships:

Recall that previously we defined:

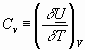
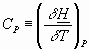
dividing expression 2) by dT and evaluating at constant P yields: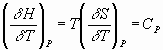

 

 

If we divide 2) by dP, evaluate at Const. T: etc.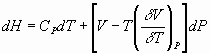

Other similarly derived physical constants include :

  1. Volume expansivity

  2. Isothermal compressibility:

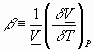
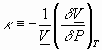
since:

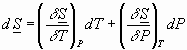
We can se our definitions:

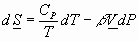
and from:

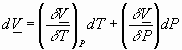
Replace b into equation 5):