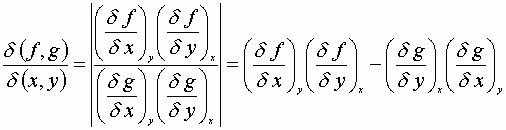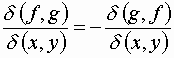Euler’s Theorem:
For a homogeneous function to degree n in x + y:
If
![]()
![]()
Then
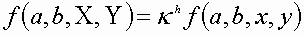
In thermo there are 2 special cases
1st detree in mass (extensive)
![]()
![]()
0th degree in mass (intensive)
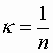
![]()
In general:
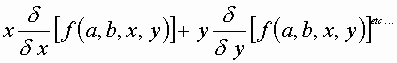
![]()
For energy:
![]()
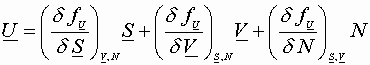
![]()
\ U is a single value state function.
Corollary – Postulate 1:
Any intensive variable can be expressed as n + 1 independent intensive variables.
N.B. = intensive & extensive variable derivatives have different meanings.
We showed earlier:
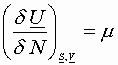
Since ![]()
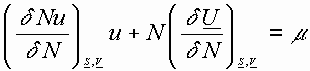
Euler’s theorem says: 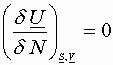
Tricks with partials:
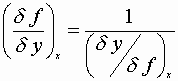
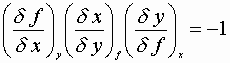
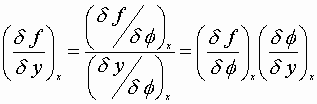
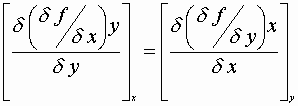
![]()